
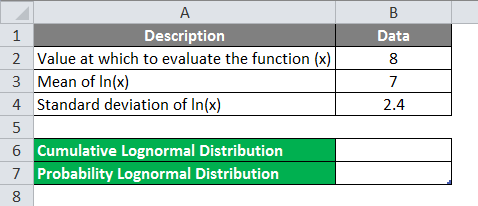
We say μ = 1.1.įind the expected value of the number of times a newborn baby’s crying wakes its mother after midnight. The number 1.1 is the long-term average or expected value if the men’s soccer team plays soccer week after week after week. The men’s soccer team would, on the average, expect to play soccer 1.1 days per week. The table helps you calculate the expected value or long-term average. Expected Value Table This table is called an expected value table. In this column, you will multiply each x value by its probability.
#Probability using mean and standard deviation excel pdf#
Construct a PDF table adding a column x* P( x). To do the problem, first let the random variable X = the number of days the men’s soccer team plays soccer per week. Find the long-term average or expected value, μ, of the number of days per week the men’s soccer team plays soccer. The probability that they play zero days is 0.2, the probability that they play one day is 0.5, and the probability that they play two days is 0.3. In other words, after conducting many trials of an experiment, you would expect this average value.Ī men’s soccer team plays soccer zero, one, or two days a week. This “long-term average” is known as the mean or expected value of the experiment and is denoted by the Greek letter μ. When evaluating the long-term results of statistical experiments, we often want to know the “average” outcome.

The Law of Large Numbers states that, as the number of trials in a probability experiment increases, the difference between the theoretical probability of an event and the relative frequency approaches zero (the theoretical probability and the relative frequency get closer and closer together). In his experiment, Pearson illustrated the Law of Large Numbers. To demonstrate this, Karl Pearson once tossed a fair coin 24,000 times! He recorded the results of each toss, obtaining heads 12,012 times. It gives information about what can be expected in the long term. As you learned in (Figure), probability does not describe the short-term results of an experiment. What is the probability that the result is heads? If you flip a coin two times, does probability tell you that these flips will result in one heads and one tail? You might toss a fair coin ten times and record nine heads. This means that over the long term of doing an experiment over and over, you would expect this average. The expected value is often referred to as the “long-term” average or mean. Note: Microsoft Excel recommends using the new VAR.S function.Mean or Expected Value and Standard Deviation VAR and VAR.S produce the exact same result. Take the square root of this result to find the standard deviation based on a sample.ģ. Note: you already knew this answer (see step 1 under STDEV.S). The VAR.S function below estimates the variance based on a sample.
Take the square root of this result to find the standard deviation based on the entire population.Ģ. Note: you already knew this answer (see step 5 under STDEV.P). The VAR.P function below calculates the variance based on the entire population. Sometimes it's easier to use the variance when solving statistical problems.ġ. Variance is the square of the standard deviation. Note: why do we divide by n - 1 instead of by n when we estimate the standard deviation based on a sample? Bessel's correction states that dividing by n-1 instead of by n gives a better estimation of the standard deviation. Fortunately, the STDEV.S function in Excel can execute all these steps for you.

Repeat steps 1-5 above but at step 5 divide by n-1 instead of N.ģ. The STDEV.S function uses the following formula: You only have the test scores of 5 students. For example, you're teaching a large group of students. The STDEV.S function (the S stands for Sample) in Excel estimates the standard deviation based on a sample. Fortunately, the STDEV.P function in Excel can execute all these steps for you. Divide by the number of data points (N = 5).ħ. For each number, calculate the distance to the mean.ģ. The STDEV.P function uses the following formula: The entire population consists of 5 data points. You have the test scores of all students. For example, you're teaching a group of 5 students. The STDEV.P function (the P stands for Population) in Excel calculates the standard deviation based on the entire population. As a result, the numbers have a high standard deviation. The numbers below also have a mean (average) of 10.Įxplanation: the numbers are spread out.
As a result, the numbers have a low standard deviation.ģ. The numbers below also have a mean (average) of 10.Įxplanation: the numbers are close to the mean.


 0 kommentar(er)
0 kommentar(er)
